Modeling Integer Programming to Multiple Target Access Problem
click for the abstract

My research introduces a new, exact solution model for the multiple target access problem, a problem in least-cost pathfinding commonly used in fields such as forestry to plan road networks. Unlike previous heuristic methods that find approximate solutions, this model guarantees the global optimal solution without simplifying assumptions.

A key innovation is its use of vector-based network configurations, making it more adaptable. Experiments confirmed the model's effectiveness in finding the optimal solution and demonstrated that adjusting solver parameters can expedite the process. The model applies to both experimental and real-world data, underscoring its practical value in road network design.

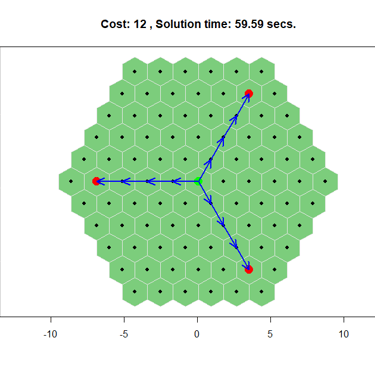
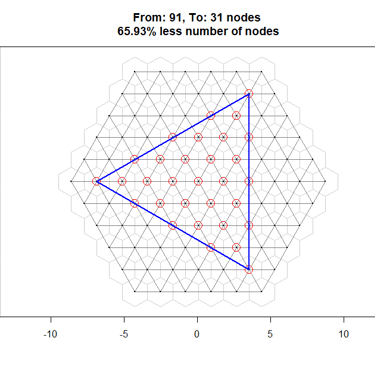
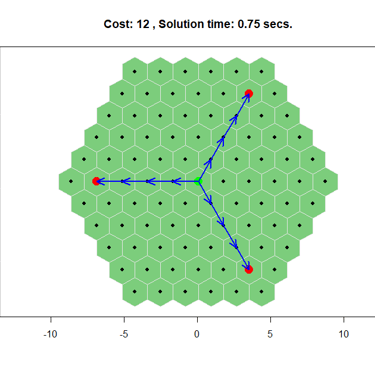
On a hexagonal tessellation graph with a single source and three targets, my algorithm initially solved the problem in under a minute. Adding a convex hull preprocess significantly reduced the computation time to under one second a 98% improvement.

All rights reserved © EK 2025